Calculate the direction angle of the mouse with CSS trigonometric functions illustrated by the sleeping monk example

This insightful project was sparked by Bramus' excellent article on trigonometric calculations in CSS¹ (along with my brief flirting with Web3, where the MetaMask fox attentively monitored my cursor movements).

Indeed, for those of us who aren't math aficionados and whose school days are but a distant memory, the practical application of trigonometric functions like sine, cosine, and tangent can pose a bit of a challenge. Hence, the motivation for a modest Tuedo Fun Project—an opportunity to revisit and refresh those long-buried skills.

The Italian author Umberto Eco once felt like poisoning a monk in his fundamental work The Name of the Rose², whereas we only want to disturb the contemplative man with a fly.

The SVG vectors of the monk and the fly are taken from the open source library svgrepo.com. An article by Keith J. Grant was very helpful for the transition of a background gradient between day and night³.

The objective of the project is to convert the movement of the mouse into an angle so that the fly (whose movement following the pointer is throttled in the Javascript file with a setTimeout function) is rotated in the direction of the mouse and the pupils of the monk's eyes fixate the disturbing fly. If there is no mouse movement, the night mode switches on after a certain time (CSS custom property --going-to-sleep) (more precisely, the night mode is the CSS standard mode, while the daylight data-theme is activated when the mouse is moved).

The atan2 function is very helpful for this, which returns the direction in degrees from the two x and y coordinates of the mouse (relative to the origin of the graph, i.e. in practical terms the old position of the mouse), values that range between -180 and 180 degrees.

The atan2() CSS function is a trigonometric function that returns the inverse tangent of two values between -infinity and infinity. The function accepts two arguments and returns the number of radians representing an <angle> between -180deg and 180deg.

mdn web docs

The following illustration shows this value range. Two values that specify the directing position are important at this point. Firstly, half of the fly width and height must be taken into account, and secondly, the --eye-correction value is used to target the position between the monk's eyes (the CSS custom property --eye-correction-without-unit is a number that is filled by JavaScript to enable this value to be calculated further in CSS).

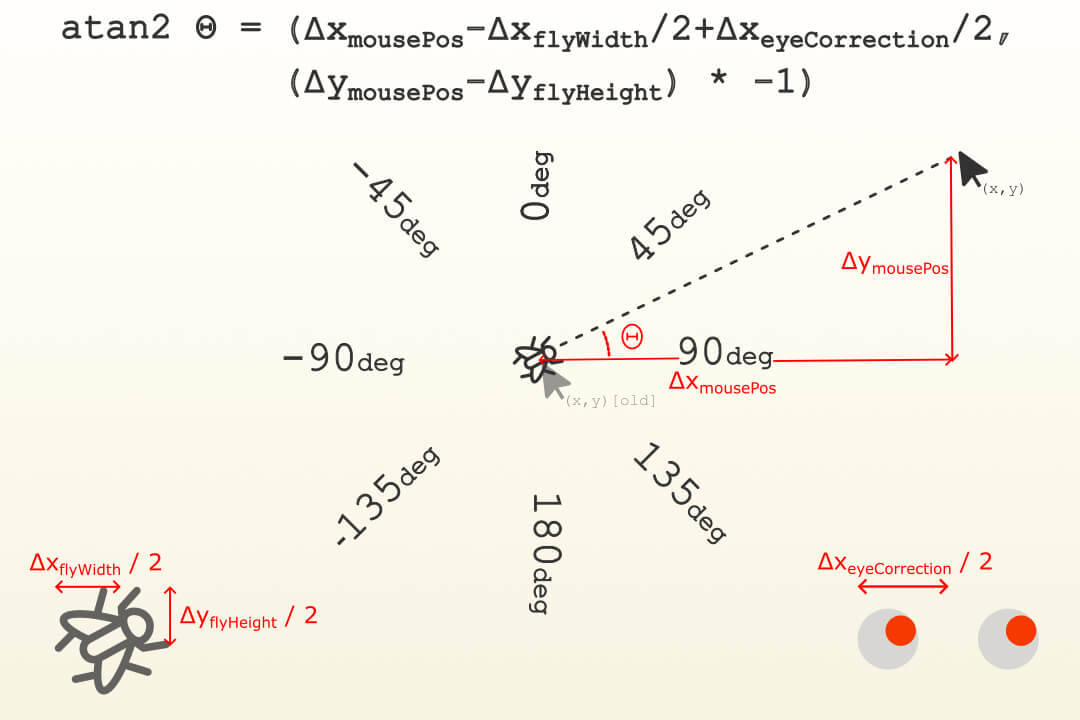
Transferred to CSS, this calculation looks like this:

/* Variables for calculation */
--calculation: atan2(calc(var(--pointer-x) - var(--my-x) - (var(--fly-width) / 2) + var(--eye-correction-without-unit)),
            calc(var(--pointer-y) - var(--my-y) - (var(--fly-height) / 2)) * -1);

Another important calculation requires the pupils of the monk's eyes moving in the direction of the stubborn fly. The atan2 function comes in handy here again, which sets the x and y coordinates of the fly relative to the centre between the monk's eyes and calculates the degree of direction using the circle number Pi. A calculation that we perform in the JavaScript file and simply transfer to the CSS custom property --pupilDegree.

/**
 * Pupils Movement
 */

let { x: myFlyX, y: myFlyY } = $myFly.getBoundingClientRect();
myFlyX += flyWidth / 2;
myFlyY += flyHeight / 2;

const calcPupilDegree = Math.atan2(myFlyX - myMonkEyesCenterX, (myFlyY - myMonkEyesCenterY) * -1);
$root.style.setProperty(`--pupilDegree`, `${(calcPupilDegree * 180) / Math.PI - 90}deg`);

Last but not least, please refer to the code in the Github repo and on CodePen, you can use the links below.